ΥΛΙΚΟ

 

Βιογραφικό της Katharine O’Brien (1922–1998)

 

Η Katharine Elizabeth O’Brien ήταν Αμερικανίδα μαθηματικός και ποιήτρια, μια προσωπικότητα που γεφύρωσε με επιτυχία το χάσμα μεταξύ θετικών επιστημών και ανθρωπιστικών σπουδών.

Σπουδές: Έλαβε το διδακτορικό της στα Μαθηματικά από το Πανεπιστήμιο Brown.

 

Καριέρα: Δίδαξε για πολλά χρόνια και διετέλεσε επικεφαλής του τμήματος Μαθηματικών στο Deering High School στο Portland του Maine.

 

Λογοτεχνικό Έργο: Τα ποιήματά της δημοσιεύτηκαν σε έγκριτα περιοδικά όπως το The New Yorker, το Scientific Monthly και το The Mathematics Teacher. Εξέδωσε δύο ποιητικές συλλογές: Excavation and Other Verse και Digging for Treasure.

 

Αναγνώριση: Ήταν γνωστή για την ικανότητά της να χρησιμοποιεί μαθηματική ορολογία με τρόπο πνευματώδη και λυρικό, κάνοντας τα μαθηματικά προσβάσιμα μέσω της τέχνης.

 

Η Katharine O’Brien καταφέρνει με το ποίημα “Valentine” κάτι μοναδικό: μετατρέπει την “ψυχρή” γλώσσα των μαθηματικών σε παιχνιδιάρικη, γεμάτη συναίσθημα ερωτική εξομολόγηση.

 

Katharine O’ Brien

 

Valentine

 

You disintegrate my differential,

you dislocate my focus.

 

My pulse goes up like an exponential

whenever you cross my locus.

 

Without you, sets are null and void-

so won’t you be my cardioid?

 

Απόδοση στα Ελληνικά:

 

Βαλεντίνος

 

Μου αποσυνθέτεις το διαφορικό,

μου μετατοπίζεις την εστία.

 

Ο σφυγμός μου ανεβαίνει εκθετικά

κάθε φορά που τέμνεις τον γεωμετρικό μου τόπο.

 

Χωρίς εσένα, τα σύνολα είναι κενά και άκυρα –

γι’ αυτό, δεν γίνεσαι η καρδιοειδής μου;

*

ΣΧΟΛΙΑ

 

Α

Το “Valentine” είναι κλασικό παράδειγμα μαθηματικής ποίησης, όπου η αυστηρή ορολογία χρησιμοποιείται ως μεταφορά για την ανθρώπινη εμπειρία.

Ανάλυση των Όρων:

Διαφορικό (Differential): Το διαφορικό σχετίζεται με την αλλαγή. Εδώ, η παρουσία του αγαπημένου προσώπου “αποσυνθέτει” τη λογική ροή και τη σταθερότητα της ποιήτριας.

 

Εστία (Focus): Στη γεωμετρία (π.χ. στις κωνικές τομές), η εστία είναι το κεντρικό σημείο αναφοράς. Η αγάπη προκαλεί “μετατόπιση” της προσοχής και της ισορροπίας.

 

Εκθετικά (Exponential): Περιγράφει μια εξαιρετικά γρήγορη αύξηση. Ο χτύπος της καρδιάς δεν αυξάνεται απλώς γραμμικά, αλλά με ρυθμό που υποδηλώνει πάθος.

 

Γεωμετρικός Τόπος (Locus): Το σύνολο των σημείων που ικανοποιούν μια συνθήκη. Η συνάντηση των δύο προσώπων περιγράφεται ως η τομή των δικών τους “τροχιών”.

 

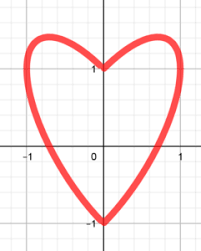
Καρδιοειδής (Cardioid): Αυτό είναι το πιο ευφυές σημείο του ποιήματος. Η καρδιοειδής είναι μαθηματική καμπύλη που το σχήμα της θυμίζει καρδιά.

 

Η O’ Brien χρησιμοποιεί την έννοια των Κενών Συνόλων (Null and void sets) για να εκφράσει τη μοναξιά και την έλλειψη νοήματος. Το ποίημα αποδεικνύει ότι τα μαθηματικά δεν είναι μόνο αριθμοί, αλλά μια γλώσσα που μπορεί να περιγράψει την πολυπλοκότητα των συναισθημάτων. Η επιλογή της καρδιοειδούς στο κλείσιμο λειτουργεί ως η τέλεια “γεωμετρική” λύση στην εξίσωση του έρωτα, συνδέοντας το σχήμα της καρδιάς με τον μαθηματικό τύπο.

 

Β

Η καρδιοειδής (cardioid) είναι μια από τις πιο γοητευτικές καμπύλες της γεωμετρίας, καθώς το όνομά της προέρχεται από την ελληνική λέξη «καρδιά» λόγω του χαρακτηριστικού της σχήματος.

Ακολουθεί μια σύντομη ανάλυση της γεωμετρίας της:

Πώς δημιουργείται

Η καρδιοειδής ανήκει στην οικογένεια των επικυκλοειδών. Φανταστείτε δύο κύκλους με την ίδια ακριβώς ακτίνα. Αν σταθεροποιήσουμε τον έναν και κυλήσουμε τον άλλον γύρω από την περιφέρειά του χωρίς να γλιστράει, το ίχνος που αφήνει ένα συγκεκριμένο σημείο της περιφέρειας του κινούμενου κύκλου σχηματίζει την καρδιοειδή.

 

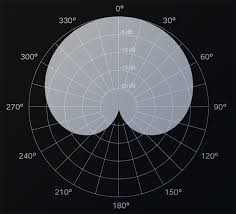
Μαθηματική Περιγραφή

Σε αντίθεση με τις περίπλοκες εξισώσεις στο καρτεσιανό σύστημα, η καρδιοειδής περιγράφεται πολύ κομψά σε πολικές συντεταγμένες:

Εξαρτάται από την ακτίνα των κύκλων που τη δημιουργούν.

Η εξίσωση δείχνει πώς η απόσταση από το κέντρο μεταβάλλεται ανάλογα με τη γωνία, δημιουργώντας αυτή την ασύμμετρη καμπύλη με τη μία αιχμή.

 

Γεωμετρικά Χαρακτηριστικά

Η Αιχμή: Είναι το σημείο όπου η καμπύλη “διπλώνει” προς τα μέσα (στο ποίημα της O’ Brien, αυτό μπορούσε να συμβολίζει το κέντρο της ύπαρξης ή της εστίας).

 

Πού τη συναντάμε στην πραγματικότητα

Στον καφέ μας: Αν φωτίσετε ένα φλιτζάνι γεμάτο καφέ από το πλάι, η αντανάκλαση του φωτός στα τοιχώματα σχηματίζει συχνά μια καρδιοειδή στον πάτο ή στην επιφάνεια.

Στην ακουστική: Τα καρδιοειδή μικρόφωνα έχουν ένα μοτίβο λήψης ήχου που μοιάζει με αυτό το σχήμα, επιτρέποντάς τους να “ακούν” κυρίως από μπροστά και να αγνοούν τους θορύβους από πίσω.

Γ

Το ποίημα της Katharine O’Brien είναι ένα μικρό αριστούργημα γιατί δεν χρησιμοποιεί τα μαθηματικά απλώς ως «διακόσμηση», αλλά ως δομικά στοιχεία της ανθρώπινης ψυχολογίας.

Ας εμβαθύνουμε λίγο περισσότερο στη σύνδεση των εννοιών:

Η «Αποσύνθεση» του Διαφορικού (Disintegrate my differential)

Στα μαθηματικά, το διαφορικό αντιπροσωπεύει μια απειροελάχιστη μεταβολή, τη βάση πάνω στην οποία χτίζουμε την κατανόηση της κίνησης και της αλλαγής.

Η μεταφορά: Όταν η ποιήτρια λέει «μου αποσυνθέτεις το διαφορικό», υπονοεί ότι η παρουσία του άλλου καταργεί τη δυνατότητά της να αναλύει τον κόσμο λογικά ή βήμα-βήμα. Η λογική της «σπάει» σε κομμάτια μπροστά στο συναίσθημα.

 

Η Εκθετική Μεταβολή (Exponential Pulse)

Η επιλογή της λέξης exponential (εκθετική) είναι η πιο δυνατή περιγραφή της απώλειας ελέγχου.

Η μαθηματική ακρίβεια: Μια εκθετική συνάρτηση αυξάνεται με ρυθμό που γίνεται όλο και πιο γρήγορος όσο μεγαλώνει η τιμή της.

Το συναίσθημα: Δεν είναι μια απλή αύξηση παλμών (γραμμική). Είναι μια κατάσταση «εκτός ελέγχου». Ο σφυγμός επιταχύνεται τόσο γρήγορα που αγγίζει τα όρια του πανικού ή του απόλυτου ενθουσιασμού.

 

Γεωμετρικός Τόπος και Τομή (Locus and Cross)

Ο γεωμετρικός τόπος (locus) είναι το σύνολο όλων των σημείων που ικανοποιούν μια συγκεκριμένη συνθήκη (π.χ. ένας κύκλος είναι ο γεωμετρικός τόπος των σημείων που απέχουν ίση απόσταση από ένα κέντρο).

Η μεταφορά: Ο «γεωμετρικός τόπος» εδώ είναι η προσωπική τροχιά της ζωής της. Όταν ο άλλος «τέμνει» (cross) αυτόν τον τόπο, δεν πρόκειται για μια τυχαία συνάντηση, αλλά για ένα μαθηματικά αναπόφευκτο σημείο επαφής δύο κόσμων.

 

Το Κενό Σύνολο (Null and Void Sets)

Στη θεωρία συνόλων, το κενό σύνολο είναι το σύνολο που δεν περιέχει κανένα στοιχείο.

Η υπαρξιακή διάσταση: Χωρίς το «ταίρι» της, η ζωή της δεν είναι απλώς μοναχική· είναι μαθηματικά κενή περιεχομένου. Όλες οι «ιδιότητες» και τα «στοιχεία» της ύπαρξής της ακυρώνονται.

 

Η Καρδιοειδής ως Λύση

Όπως είδαμε, η καρδιοειδής είναι μια καμπύλη που κλείνει στον εαυτό της, δημιουργώντας ένα σχήμα προστασίας και αγκαλιάς.

Στο πλαίσιο του ποιήματος, η πρόσκληση «be my cardioid» είναι μια πρόσκληση για σύγκλιση. Η καρδιοειδής έχει μια μοναδική «αιχμή» όπου η καμπύλη επιστρέφει στο σημείο μηδέν, συμβολίζοντας ίσως την επιστροφή στην κοινή τους εστία.

 

Γιατί είναι σημαντικό αυτό το ποίημα

Συχνά θεωρούμε τα μαθηματικά «κρύα» και την ποίηση «θερμή». Η O’ Brien αποδεικνύει ότι:

Αφενός τα μαθηματικά έχουν αισθητική κομψότητα, αφετέρου η αγάπη μπορεί να περιγραφεί με (μαθηματική) ακρίβεια, χωρίς να χάσει τον ρομαντισμό της.

 

 

 

 

Δημήτρης Γαβαλάς