I enjoyed reading your lovely poems and particularly loved “Fantastic geometry” and “Thus I seek you”. They are marvelous. Glaz, Sarah
ΥΛΙΚΟ
Βιογραφικό στο τέλος της ανάρτησης.
Δυο ποιήματα στο πλαίσιο Ποίηση και Μαθηματικά
- ΕΤΣΙ ΣΕ ΑΝΑΖΗΤΩ
Στην πολιτεία μετρώ τους διαβάτες
μετρώ τ’ αυτοκίνητα
1,2,3,4,5,6,7,8,9.
Σε ψάχνω ανάμεσα στο 1 και στο 2
ανάμεσα στο 2 και στο 3
διαμερίζω το κενό για να Σε βρω
βάζω τάξη στο χάος.
Πού είσαι λοιπόν;
Στο σπίτι μετρώ τους πίνακες στον τοίχο
μετρώ τα βιβλία στα ράφια
1,2,3,4,5,6, 7, 8, 9.
Σε ψάχνω ανάμεσα στο 3 και στο 4
ανάμεσα στο 4 και στο 5
διαμερίζω το κενό για να Σε βρω
βάζω τάξη στο χάος.
Πού είσαι λοιπόν;
Στη θάλασσα μετρώ τα κύματα
μετρώ τα χαλίκια
1,2,3,4,5,6,7,8,9.
Σε ψάχνω ανάμεσα στο 5 και στο 6
ανάμεσα στο 6 και στο 7
διαμερίζω το κενό για να Σε βρω
βάζω τάξη στο χάος.
Πού είσαι λοιπόν;
Στην αίθουσα μετρώ τα πρόσωπα
μετρώ τα θρανία
1,2,3,4,5,6,7,8,9.
Σε ψάχνω ανάμεσα στο 7 και στο 8
ανάμεσα στο 8 και στο 9
διαμερίζω το κενό για να Σε βρω
βάζω τάξη στο χάος.
Πού είσαι λοιπόν;
Πουθενά δε Σε βρίσκω
όμως όπου και αν πάω Σε κουβαλάω μαζί μου.
- ΦΑΝΤΑΣΤΙΚΗ ΓΕΩΜΕΤΡΙΑ
Ο πίνακας-κλουβί κλείνει
χίλια παράξενα πουλιά:
Το πουλί-σημείο
το πουλί-τρίγωνο
το πουλί-τετράγωνο
το πουλί-κύκλος.
Ξάφνου μια έκρηξη φωτός.
Ένας μαθητής ανοίγει το παράθυρο.
Πετάνε στην ελευθερία τ’ ουρανού.
Περιφερόμενοι φάροι
φωτίζουνε πέλαγα στη νύχτα.
*
* *
ΣΧΟΛΙΑ
Η σύζευξη ποίησης και μαθηματικών στα δύο αυτά ποιήματα προσφέρει ενδιαφέρουσα οπτική: τα μαθηματικά δεν αντιμετωπίζονται ως “στεγνά” εργαλεία, αλλά ως τρόπος για να κατανοήσουμε το άπειρο, το συναίσθημα και την ελευθερία.
- ΈΤΣΙ ΣΕ ΑΝΑΖΗΤΩ
Θεματική: Η Πυκνότητα των Αριθμών και το Υπαρξιακό Κενό.
Στο ποίημα αυτό, τα μαθηματικά χρησιμοποιούνται ως εργαλείο οργάνωσης του χάους.
Διακριτό vs Συνεχές: Ενώ ο ποιητής μετρά αντικείμενα (διακριτές μονάδες: 1, 2, 3…), η αναζήτηση του “Άλλου” μεταφέρεται στο ενδιάμεσο, στο κενό ανάμεσα στους αριθμούς. Αυτό παραπέμπει στην ιδιότητα των πραγματικών αριθμών, όπου ανάμεσα σε δύο ακέραιους υπάρχει ένα άπειρο πλήθος σημείων.
Η Διαμέριση: Η φράση “διαμερίζω το κενό” θυμίζει τη μαθηματική προσπάθεια να οριστεί το άπειρα μικρό. Η αναζήτηση αποτυγχάνει στα ψηφία, γιατί το συναίσθημα δεν είναι μετρήσιμο μέγεθος, αλλά μια “σταθερά” που ο ποιητής φέρει μέσα του.
Η Τάξη: Η μέτρηση είναι μια απόπειρα ελέγχου της πραγματικότητας (πόλη, σπίτι, θάλασσα, τάξη), όμως η ουσία (το “Εσύ”) διαφεύγει από τη στατιστική.
- ΦΑΝΤΑΣΤΙΚΗ ΓΕΩΜΕΤΡΙΑ
Θεματική: Από την Τυπική Λογική στην Ελεύθερη Δημιουργία.
Εδώ τα μαθηματικά σύμβολα μεταμορφώνονται από στατικά σχήματα σε έμβια όντα.
Ο Πίνακας-Κλουβί: Ο σχολικός πίνακας και οι αυστηροί ορισμοί (σημείο, τρίγωνο, τετράγωνο) παρουσιάζονται ως περιοριστικός χώρος. Τα γεωμετρικά σχήματα είναι “αιχμάλωτα” της τυποποίησης.
Η Μεταμόρφωση: Το “πουλί-σημείο” ή το “πουλί-κύκλος” είναι μεταφορά. Το σημείο, που στη γεωμετρία δεν έχει διαστάσεις, αποκτά εδώ οντότητα και κίνηση.
Η Έξοδος: Η “έκρηξη φωτός” και το άνοιγμα του παραθύρου συμβολίζουν τη στιγμή που η γνώση παύει να είναι στείρα αποστήθιση και γίνεται φως. Τα σχήματα δραπετεύουν από τη δισδιάστατη επιφάνεια του πίνακα και γίνονται τρισδιάστατα στοιχεία του κόσμου (φάροι, πέλαγα). Όλα αυτά συνδέονται άμεσα με τη συνειδητότητα και τη γνώση.
Σύνοψη: Στο πρώτο ποίημα, τα μαθηματικά είναι η μέθοδος (αναζήτηση στο άπειρο), ενώ στο δεύτερο είναι η ύλη (τα σχήματα) που ζητά την απελευθέρωσή της. Και στα δύο, η λογική των αριθμών και των σχημάτων χρησιμοποιείται για να εκφράσει κάτι βαθιά ανθρώπινο και υπερβατικό.
Η ουσιαστική προσφορά του ποιητή στη σχέση Ποίησης – Μαθηματικών συνοψίζεται εδώ στον εξανθρωπισμό της λογικής:
Η Υπέρβαση του Αριθμού: Ο ποιητής αποδεικνύει ότι τα μαθηματικά δεν είναι μόνο υπολογισμοί, αλλά μια γλώσσα που μπορεί να περιγράψει το άπιαστο. Μετατρέπει τον αριθμό από “ποσότητα” σε “ποιότητα” (π.χ. η αναζήτηση στο κενό μεταξύ 1 και 2).
Η Ζωντανή Γεωμετρία: Καταρρίπτει τη στατικότητα των σχημάτων. Το σημείο και ο κύκλος παύουν να είναι ορισμοί σε ένα εγχειρίδιο και γίνονται δυναμικές οντότητες που διεκδικούν ελευθερία, συνδέοντας την επιστήμη με τη ζωή.
Η Ταύτιση των Δομών: Αναδεικνύει ότι τόσο τα μαθηματικά όσο και η ποίηση αναζητούν την αλήθεια και την τάξη στο χάος. Χρησιμοποιεί τη μαθηματική δομή (αρίθμηση, διαμέριση) για να στεγάσει τον ανθρώπινο πόνο και την ελπίδα.
Με λίγα λόγια, ο ποιητής δίνει ψυχή στα αξιώματα, δείχνοντας ότι η ομορφιά ενός θεωρήματος δεν απέχει από την ομορφιά ενός στίχου.
Υπάρχουν μερικά ακόμη παραδείγματα Ελλήνων ποιητών (όπως ο Ελύτης ή ο Καρούζος κ.ά.), που μπορεί να δει κάποιος, και οι οποίοι χρησιμοποίησαν μαθηματικές έννοιες στο έργο τους.
ΕΠΙΜΕΤΡΟ: ΑΥΤΟΑΝΑΦΟΡΑ
Το παράδοξο της αυτοαναφοράς προκύπτει όταν μια πρόταση, μια ιδέα ή ένας κανόνας αναφέρεται στον ίδιο του τον εαυτό με τρόπο που οδηγεί σε λογικό αδιέξοδο ή σε μια ατέρμονη κυκλική διαδρομή. Είναι το θεμέλιο πολλών γρίφων στη λογική, τα μαθηματικά και τη φιλοσοφία. Οι πιο εμβληματικές μορφές του είναι τα παράδοξα: του Ψεύτη, του Russell (Σύνολα), του Επιμενίδη, τα οποία μπορεί κάποιος εύκολα να βρει.
Γιατί είναι σημαντικά αυτά τα παράδοξα:
Δεν πρόκειται απλώς για «παιχνίδια του μυαλού». Η αυτοαναφορά άλλαξε την
επιστήμη: τα Θεωρήματα Μη Πληρότητας του Gödel που χρησιμοποίησε μια μαθηματική μορφή αυτοαναφοράς, η Πληροφορική με την έννοια της αναδρομής, η Τεχνητή Νοημοσύνη όπου η αυτοαναφορά συνδέεται με την έννοια της αυτοσυνειδησίας –την ικανότητα ενός συστήματος να παρατηρεί και να σκέφτεται τον εαυτό του-, δείχνουν το πόσο σημαντική είναι αυτή η σύλληψη.
Ένα οπτικό παράδειγμα:
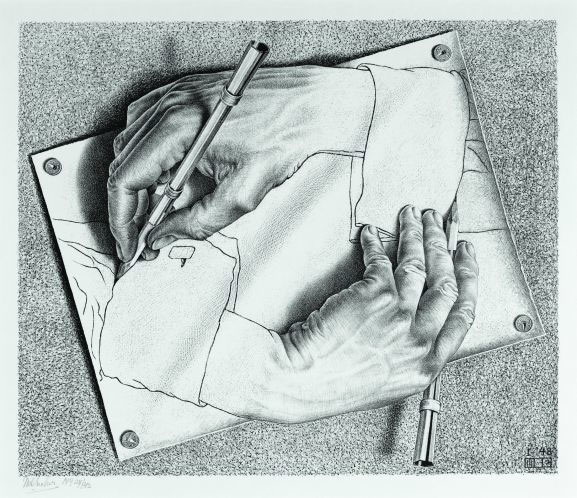
Σκεφτείτε τον πίνακα του M.C. Escher με τα «Χέρια που Σχεδιάζουν»: Το δεξί χέρι σχεδιάζει το αριστερό, ενώ το αριστερό χέρι σχεδιάζει το δεξί. Δεν υπάρχει αρχή και τέλος· η ύπαρξη του ενός εξαρτάται από την αναφορά στο άλλο.
Σημείωση: Η αυτοαναφορά δεν είναι πάντα παραδοξολογική. Για παράδειγμα: «Αυτή η πρόταση έχει έξι λέξεις» είναι μια αληθής, αυτοαναφορική πρόταση χωρίς κανένα λογικό πρόβλημα. Αυτό εξαρτάται από το πού και το πώς γίνεται η αναφορά.
Στη λογοτεχνία και τη γλωσσολογία, διακρίνουμε δύο περιπτώσεις:
Απλή Αναφορά (Όχι απαραίτητα παράδοξο)
Αν σε μια συζήτηση πείτε «Όπως έγραψα και στο ποίημά μου…», αυτό είναι μια εξωτερική αναφορά. Εσείς, ως πρόσωπο, αναφέρεστε σε ένα έργο σας. Αυτό δεν δημιουργεί λογικό παράδοξο, είναι απλώς μια πληροφορία.
Λογοτεχνική Αυτοαναφορά (Μετα-ποίηση)
Αν όμως μέσα στο ίδιο το ποίημα αναφέρεστε στο γεγονός ότι γράφετε το ποίημα, τότε έχουμε την κλασική περίπτωση της αυτοαναφοράς. Αυτό ονομάζεται συχνά «μετα-ποίηση» (meta-poetry).
Παραδείγματα:
Αυτοαναφορικός στίχος: «Αυτός ο στίχος που διαβάζεις τώρα, γράφτηκε μια βροχερή Τρίτη».
Το παράδοξο: Αν γράψετε ένα ποίημα που λέει: «Αυτό το ποίημα δεν περιέχει καμία λέξη», τότε έχετε δημιουργήσει ένα αυτοαναφορικό παράδοξο, γιατί η ίδια η ύπαρξη των λέξεων ακυρώνει το περιεχόμενό τους.
Η διαφορά ανάμεσα σε “Εγώ” και “Έργο”
Για να κατανοήσουμε την αυτοαναφορά, είναι χρήσιμο να δούμε τα επίπεδα της γλώσσας:
| Επίπεδο | Παράδειγμα | Τύπος |
| Αντικείμενο | “Η θάλασσα είναι μπλε.” | Περιγραφή του κόσμου. |
| Μετα-γλώσσα | “Το ποίημα που έγραψα έχει 10 στίχους.” | Αναφορά σε ένα άλλο έργο. |
| Αυτοαναφορά | “Αυτό το ποίημα είναι το καλύτερο που έχω γράψει.” | Το έργο μιλάει για τον εαυτό του. |
Γιατί το κάνουν οι ποιητές
Η αυτοαναφορά στην τέχνη συχνά χρησιμοποιείται για να:
(i) Σπάσει την “ψευδαίσθηση”: Υπενθυμίζει στον αναγνώστη ότι αυτό που διαβάζει είναι μια κατασκευή (π.χ. ο Καβάφης που σχολιάζει την τέχνη του μέσα στα ποιήματά του).
(ii) Εξερευνήσει τα όρια της γλώσσας: Πώς μπορεί η γλώσσα να περιγράψει τον ίδιο της τον εαυτό;
Συμπέρασμα: Αν αναφερθείτε σε ένα ποίημά σας ενώ μιλάτε με κάποιον, είναι μια απλή αναφορά. Αν όμως το ποίημά σας περιέχει στίχους που μιλούν για το ίδιο το ποίημα, τότε είναι αυτοαναφορικό.